Calculate the Conditional Chance utilizing a Contingency Desk
[ad_1]
A conditional chance incorporates a situation which forces you to focus your consideration to a subset of the pattern area. For instance, an organization could have men and women working for the corporate. Nonetheless, chances are you’ll need to reply questions on males solely or females solely. In case you are coping with insurance coverage, chances are you’ll need to reply questions on people who smoke solely or non-smokers solely.
A great way to get began with conditional chances is to make use of a contingency desk.
Conditional chance utilizing a contingency desk
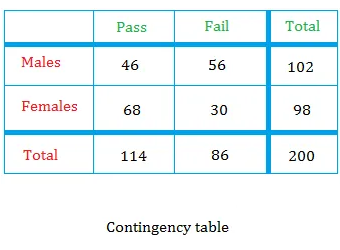
Right here is the best way to discover the conditional chance utilizing a contingency desk that we used within the lesson about marginal chance. The desk reveals check outcomes for 200 college students who took a GED check.

From the record of 200 college students, we choose a pupil randomly. Nonetheless, suppose that you simply already know the coed chosen is a male.
The truth that the coed is a male implies that the occasion has already occurred. And it forces you to focus your consideration solely on males or 102 attainable outcomes.
What’s conditional chance?
Figuring out that the pupil is a male, you’ll be able to calculate the chance that this pupil has handed or failed. This sort of chance is known as conditional chance
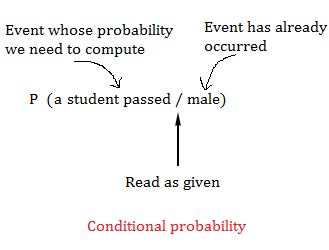
The notation to seek out the chance that ‘a pupil has handed if the coed is male is
P(a pupil has handed / male)
You may actually compute any of the next 8 conditional chances:
- P(a pupil has handed / male)
- P(a pupil has handed / feminine)
- P(a pupil has failed / male)
- P(a pupil has failed / feminine)
- P(a pupil is male / handed)
- P(a pupil is male / failed)
- P(a pupil is feminine / handed)
- P(a pupil is feminine / failed)
A few examples displaying the best way to discover the conditional chance utilizing a contingency desk
Instance #1
Allow us to compute the P(a pupil has handed / male).
If the coed is male, then the coed will probably be picked from the record of 102 males.
From this record solely 46 college students have handed.

Variety of males who handed
Complete variety of males
46
102
= 0.451
Instance #2
What about P(a pupil is male / handed) ?
The variety of college students who handed is the same as 114.
From this record, solely 46 college students are males.
a pupil is a male
Variety of college students who handed
46
104
= 0.403
As you’ll be able to see from the outcomes P(a pupil has handed / male) isn’t equal to
P(a pupil is male / handed) as a result of there’s a distinction.
P(a pupil has handed / male): This chance simply reveals the success charge of males solely.
P(a pupil is male / handed): This chance compares the success charge of males to females.
Conditional chance formulation
Take an in depth look once more on the following ratio:
Variety of males who handed
Complete variety of males
Let M be the occasion ‘the coed is a male’
Let P be the occasion ‘the coed has handed’
Let P∩M be the occasion ‘the coed is a male and has handed’
n(P∩M) = variety of male college students who handed = 46
n(M) = whole variety of male college students = 102
n(P ∩ M)
n(M)
46
102
= 0.451
We are able to get the identical reply utilizing chance as a substitute of counting. Divide the numerator and the denominator of the ratio instantly above by 200.
46 / 200
102 / 200
0.23
0.51
= 0.451
P(P∩M) = chance {that a} pupil has handed if the coed is male = 46 / 200 = 0.23
P(M) = chance {that a} pupil is male = 102 / 200 = 0.51
P(P ∩ M)
P(M)
We are able to then conclude that there are two methods to discover a conditional chance.
Methods to discover the conditional chance by counting
In case you are coping with equally possible outcomes equivalent to tossing a coin or a good die with six sides, then for any two occasions A and B, you should use the next formulation:
n(A ∩ B)
n(B)
Methods to discover the conditional chance by utilizing the definition of conditional chance
Whether or not you might be coping with equally possible outcomes or not, then for any two occasions A and B, you should use the next formulation:
P(A ∩ B)
P(B)
The chance of A given B is the ratio of the chance of the intersection of A and B to the chance of B.
Extra examples of conditional chance
Instance #3
A card is drawn at random from an ordinary deck. The cardboard isn’t changed. Discover the chance that the second card is a king provided that the primary card drawn was a king.
Let K1 be occasion ‘the primary card drawn is a king’ and K2 be the occasion ‘the second card drawn is a king’
If a king is drawn and never changed, then there are 3 kings left and the deck will now have 51 playing cards.
P(K2 / K1) = 3/51 ≈ 0.0588
Two occasions A and B are referred to as impartial occasions if P(A / B) = P(A)
Instance #4
Let H1 be the occasion that the primary toss of a coin is a head and let H2 be the occasion that the second toss of the coin is a head. Present that H1 and H2 are impartial occasions.
Your calculations should present that P(H2 / H1) = P(H2)
The complete pattern area is {HH, HT, TH, TT}
H2 = {HH, TH} and P(H2) = 0.50
Provided that the primary toss is a head, we find yourself with {HH, HT} and we’re restricted to those two outcomes to compute P(H2 / H1)
From these two outcomes, we see that HH (half of the two outcomes) has a head because the second toss.
P(H2 / H1) = 0.5
P(H2 / H1) = P(H2) = 0.5, and thus H1 and H2 are impartial occasions.
In impartial occasions, the prevalence of an occasion doesn’t affect the prevalence of one other occasion. In instance #4, the occasion ‘you get a head with the primary toss or H1’ won’t affect the chance of getting once more a head with the second toss.
This isn’t the case with instance #3 the place the prevalence of an occasion can affect the prevalence of one other.
Two occasions A and B are referred to as dependent occasions if P(A / B) ≠ P(A)
In instance #3, P(K2 / K1) = 3/51. Nonetheless, P(K2) = 4/52 = 0.076
Because the first card was not changed or put again within the deck, the chance of the second draw clearly will depend on the end result of the primary,
[ad_2]