45-45-90 Triangle
[ad_1]
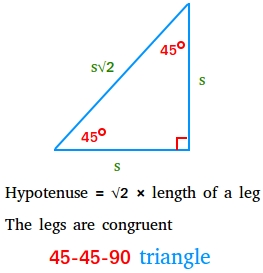
A forty five-45-90 triangle, additionally known as isosceles proper triangle, is a particular proper triangle through which each legs are congruent and the size of the hypotenuse is the sq. root of two occasions the size of a leg.
Hypotenuse = √2 × size of a leg
The legs are congruent

Wanting fastidiously on the determine above, you will have noticed the next ratios:
Suppose we begin from the smallest angle to the biggest angle and from the shortest facet to the longest facet
The angles of a 45-45-90 triangle are within the ratio 1:1:2
The perimeters of a 45-45-90 triangle are within the ratio 1:1:√2
45-45-90 triangle proof
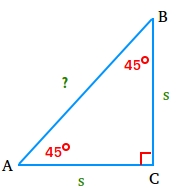
Begin with an isosceles proper triangle ABC just like the one proven above.
Let phase AB equal to x and use the Pythagorean theorem to search out the size of phase AB.
AB2 = AC2 + BC2
x2 = s2 + s2
x2 = 2s2
x = √(2s2)
x = (√2)[√(s2)]
x = (√2)(s)
x = s√2
Examples of 45-45-90 triangles
Instance #1: 1, 1, √2
Every leg is the same as 1
Hypotenuse: √2
Instance #2: 2, 2, 2√2
Every leg is the same as 2
Hypotenuse: 2√2
Instance #3: 3, 3, 3√2
Every leg is the same as 3
Hypotenuse: 3√2
Utilizing the size of 1 facet to resolve a 45-45-90 triangle
Instance #4:
The hypotenuse of a 45-45-90 triangle is 7√2. Discover the lengths of the opposite sides.
Hypotenuse = s√2, s is the size of a leg.
7√2 = s√2
Divide each side by √2.
7√2 / √2 = s√2 / √2
7 = s
The legs of this 45-45-90 triangle have a size of seven
Instance #5:
The legs of a 45-45-90 triangle have a size of 13. Discover the size of the hypotenuse.
Hypotenuse = s√2, s is the size of a leg.
The size of the hypotenuse is 13√2
Utilizing the 45-45-90 triangle to resolve real-world issues
Instance #6:
The space from first base to second base of a baseball discipline is normally 90 ft though this distance could differ. Discover the space from dwelling plate to the second base.
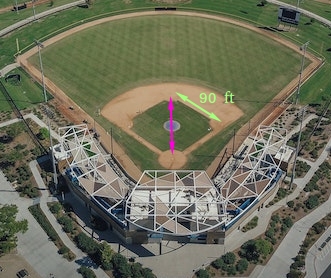
The space x from dwelling plate to the second base is the size of the hypotenuse of a 45-45-90 triangle as proven within the determine under.
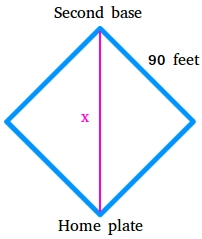
Hypotenuse = s√2, s is the size of a leg.
For the reason that distance from first base to second base is 90 ft, s is the size of the leg of the 45-45-90 diploma triangle.
Hypotenuse = s√2
Hypotenuse = 90√2
Hypotenuse = 127.278
The space from dwelling plate to the second base is 127.278 ft.
Instance #7:
A gardener desires to make a sq. backyard whose diagonal is the same as 45√2 ft . What’s the perimeter of the backyard?
First, that you must discover the size of every facet of the sq. utilizing the method under.
Hypotenuse = s√2, s is the size of a leg.
45√2 = s√2
Divide each side by √2 to search out the s
45√2 / √2 = s√2 / √2
s = 45 ft
The size of every facet is 45 ft.
The perimeter of the sq. is 45 + 45 + 45 + 45 = 90 + 90 = 180
The perimeter of the sq. is 180 ft.
Space of a 45-45-90 triangle
Discovering the realm of a 45-45-90 triangle may be very simple. If s is the size of a leg, then, the realm of a 45-45-90 triangle is s2
Instance #8:
Discover the realm of a 45-45-90 triangle if the size of a leg is 25√3
Space = s2 = (25√3)2
Space = (25)2(√3)2
Space = 625(√3)(√3)
Space = 625(√9)
Space = 625(3)
Space = 1875
[ad_2]