Circumference of a circle – Definition, components, Actual-World Examples
[ad_1]
The circumference of a circle, additionally referred to as the perimeter of a circle, is the gap round a circle or any round object corresponding to a clock, a pizza, or a dinner plate. For instance, the gap round a round clock is the circumference of the clock.

The right way to discover the circumference of a circle?
Technique 1:
You can use a versatile measuring tape just like the one used within the picture above to measure the perimeter of the clock. As you wrap the tape measure across the clock, simply stretch the measuring tape as a lot as attainable so the measurement will be as correct as attainable. Then, learn the quantity you see on the measuring tape.
Technique 2
Mark a degree on the margin of any round object. That is proven beneath with a vertical purple mark. Roll the round object both to the left or to the fitting till it makes one revolution. The gap between the vertical purple marks is the circumference of the round object.
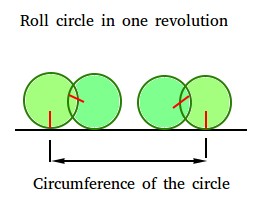
Technique 3
One other solution to discover the perimeter of a circle or any round object is to make use of a particular components.
Circumference components
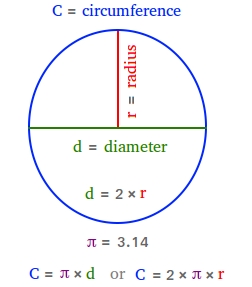
The perimeter of the circle will be discovered utilizing both C = πd = π × d or C = 2 × π × r.
Pi or π is a particular mathematical fixed, and the worth of pi is roughly equal to 22/7 or 3.14. The explanation that we use 3.14 is as a result of pi is an irrational quantity with limitless digits after the decimal level. The lesson about the quantity π will let you know extra about pi. It is going to additionally reveals the way to derive the components and clarify why the circle’s circumference is C = π × d or C = 2 × π × r.
If both the radius of a circle (r) or the diameter of a circle (d) is thought, you could find the circumference by merely substituting the recognized worth for r or d within the components.
The circumference is expressed in linear models.
- If r or d is measured in meters, then the circumference can also be measured in meters or m.
- If r or d is measured in kilometers, then the circumference is measured in kilometers or km.
- If r or d is measured in inches, then the circumference is measured in inches or in.
The right way to discover circumference of a circle utilizing the diameter?
The product of the fixed π and the diameter of the circle is the same as the circumference of the circle.
C = π × d
You simply have to seek out the size of the diameter and them multiply by 3.14 to get the circumference. To get the diameter, use a ruler or a measuring tape. Measure from one fringe of the circle to a different edge ensuring that you simply undergo the midpoint or heart of the circle (or clock). After I measured the diameter of the clock you see beneath, I discovered one thing near 11.90 inches.

C = 3.14 × d = 3.14 × 11.9 = 37.36 inches. Wanting on the measuring tape across the clock, we will see that the circumference is certainly near 37.3 inches!
The right way to discover circumference of a circle utilizing the radius?
Twice the product of the fixed π and the radius of the circle is the same as the circumference of the circle.
C = 2π × r
You simply have to seek out the size of the radius r and them multiply by 2 after which by 3.14 to get the circumference. To get the radius, measure from the middle of the circle(or clock) to the sting of the circle. After I measured the radius of the clock you see beneath, I discovered one thing shut to five.95 inches.

C = 2(3.14) × r = 2(3.14) × 5.95 = 37.36 inches. Once more, wanting on the measuring tape across the clock, we will see that the circumference is certainly near 37.3 inches!
A number of extra examples exhibiting the way to discover the circumference of a circle
Examples #1
Calculate the circumference of a circle if r = 2 inches
C = 2 × π × r = 2 × 3.14 × 2 = 12.56 inches
Examples #2
Calculate the circumference of a circle if r = 4 inches
C = 2 × π × r = 2 × 3.14 × 4 = 25.12 inches
Examples #3
If D = 10 centimeters, discover the circumference.
You might have two selections. You possibly can first discover r after which substitute its worth for r within the components.
r is half the diameter, so r = 10 divided by 2
r = 5 cm
C = 2 × π × r = 2 × 3.14 × 5 = 31.4 cm
In any other case, you’ll be able to simply use the components C = π × D
C = 3.14 × 10 = 31.4 cm
A difficult train in regards to the circumference of a circle
Examples #4
The circumference of circle A is 4 occasions the circumference of circle B
The diameter of circle B is 7. What’s the diameter of circle A?
Let CA be the circumference of circle A
Let CB be the circumference of circle B
Let DA be the diameter of circle A
Let DB be the diameter of circle B
Because the ratio of circumference to diameter is similar for all circles, you should utilize the next proportion to unravel this drawback.
Issues that we all know:
CA = 4 × CB
DB = 7
Exchange these within the proportion
|
=
8 then, 2 × 20 = 5 × 8 |
|
=
CB then, 4 × CB × 7 = DA × CB |
28 × CB = DA × CB
Divide each side by CB
DA = 28
Issues that we all know:
CA = 4 × CB
DB = 7
Exchange these within the proportion
|
=
8 then, 2 × 20 = 5 × 8 |
Then, 4 × CB × 7 = DA × CB
28 × CB = DA × CB
Divide each side by CB
DA = 28
The right way to calculate the circumference if the world is given
C = 2π × r
A = π × r2
Clear up for r utilizing A = πr2.
r2 = A/π
r = √(A/π)
Substitute √(A/π) for r in C
C = 2π × √(A/π)
C = 2√(π)2 × √(A/π)
C = 2√[(π)2 × (A/π)]
C = 2√[(π)×(A)]
Circumference of a circle quiz. See how nicely you’ll be able to calculate the circumference or perimeter of a circle
[ad_2]