Divide on a Quantity Line | Numerous Division Issues
[ad_1]
How one can divide on a quantity line?
Study to divide
utilizing quantity line to search out the quotient.
We are able to do repeated subtraction on the quantity line to search out division.
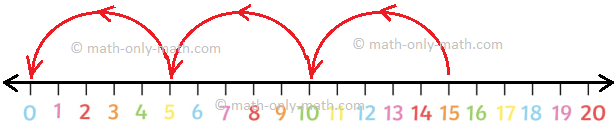
Allow us to discover 15 ÷ 5.
Thus, 15 ÷ 5 = 3
Solved Examples to point out Divide on a
Quantity Line:
1. Remedy 14 ÷ 7
Answer:
7 is subtracted
repeatedly from 14 utilizing the quantity line
When 7 is subtracted 2 occasions from 14 within the quantity line, then we get the rest zero.
Thus, 7 is subtracted from 14, 2 occasions.
Therefore, 14 ÷ 7 = 2, 2 is the quotient.
2. Divide 40 ÷ 8
Utilizing the quantity
line 8 is subtracted repeatedly from 40
When 8 is subtracted
5 occasions from 40 within the quantity line, then we get the rest zero.
Thus, 8 is
subtracted from 40, 5 occasions.
Therefore, 40 ÷ 8 =
5, 5 is the quotient.
3. Remedy 24 by 6
Answer:
6 is subtracted
repeatedly from 24 utilizing the quantity line
When 6 is
subtracted 4 occasions from 24 within the quantity line, then we get the rest zero.
Thus, 6 may be
subtracted from 24, 4 occasions.
Therefore, 24 ÷ 6 =
4, 4 is the quotient.
4. Divide 15 ÷ 3
3 is subtracted
repeatedly from 15 utilizing the quantity line
3 is subtracted
from 15, 5 occasions within the quantity line, then we get the rest zero.
Thus, 3 may be
subtracted from 15 5 occasions.
Therefore, 15 ÷ 3 = 5,
5 is the quotient.
5. Divide 63 ÷ 9
9 is subtracted
repeatedly from 63 utilizing the quantity line
9 is subtracted
from 63, seven occasions within the quantity line, then we get the rest zero.
Thus, 9 may be
subtracted from 63 seven occasions.
Therefore, 63 ÷ 9 = 7,
7 is the quotient.
On the quantity line, we are able to present repeated subtraction by counting backward in equal jumps.
6. Divide 12 by 2.
Begin from 12. Soar backwards by taking jumps of two steps every. Cease at 0.
Observe that 6 jumps are wanted to achieve 0.
12 – 2 = 10; 10 – 2 = 8; 8 – 2 = 6; 6 – 2 = 4; 4 – 2 = 2; 2 – 2 = 0
Divide 6 by 3.
We write: 12 ÷ 2 = 6
We learn: 12 divided by 2 equals 6.
7. Divide 15 by 5.
Begin from 15. Soar backwards by taking jumps of 5 steps every. Cease at 0.
Observe that 3 jumps are wanted to achieve 0.
15 – 5 = 10; 10 – 5 = 5; 5 – 5 = 0
We write: 15 ÷ 5 =3
We learn: 15 divided by 5 equals 3.
The above examples will assist us to resolve numerous division issues on 1-digit quantity and 2-digit quantity by a single digit quantity utilizing quantity line.
Questions and Solutions on Division on a Quantity Line:
1. Use the quantity line to search out the division by repeated subtraction.
(i) Discover 12 ÷ 2
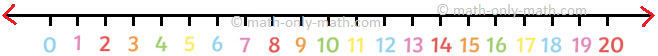
12 ÷ 2 = _____
(ii) Discover 18 ÷ 3
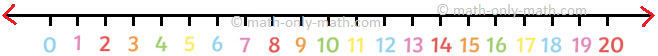
18 ÷ 3 = _____
(iii) Discover 20 ÷ 4
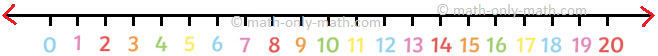
20 ÷ 4 = _____
Reply:
(i) 12 ÷ 2 = 6
(ii) 18 ÷ 3 = 6
(iii) 20 ÷ 4 = 5
From Divide on a Quantity Line to HOME PAGE
Did not discover what you have been in search of? Or wish to know extra info
about Math Solely Math.
Use this Google Search to search out what you want.
[ad_2]
You may also like
Idea of Sample | Related Patterns in Arithmetic
