Évariste Galois and His Principle
[ad_1]
* Oct. twenty fifth, 1811 † Could thirty first, 1832
… or why squaring the circle is doomed.
Galois died in a duel on the age of twenty. But, he gave us what we now name Galois concept. It decides all three historical classical issues, squaring the circle, doubling the dice, and partitioning angles into three equal components, all with a compass and ruler alone. Galois concept additionally tells us that there isn’t a common formulation to unravel the integer equation
$$
x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5=0
$$
All outcomes are adverse. A compass and ruler are usually not sufficient to assemble a sq. with the identical space as a given circle, to assemble a dice that has twice the quantity of a given one, to assemble the third a part of an arbitrary given angle, or to search out zeros of arbitrary integer polynomials of diploma 5 or larger. It has a purpose that they’ve been undecided for hundreds of years. They’re unsolvable. Since Galois, we all know why. The next article explains why with out exploring Galois concept intimately, and with a minimal of the idea of Galois teams. The primary purpose is certainly rapidly informed.
Basic Theorem of Galois Principle
The intermediate fields of a Galois extension correspond inclusion reversing to the subgroups of its Galois group.
As is so usually the case, the satan is within the particulars, and Galois’s wording has actually been far more sophisticated. In reality, the (lifeless) teenager has been largely ignored, e.g. by Gauß or Jacobi. It was not till Liouville in 1843 he acknowledged the significance and noticed the reference to Cauchy’s concept of permutations and printed them in his journal. The main points, on this case, are to point out that the issues are equal to the development of sure Galois extensions. So the explanation why all these issues are unsolvable are easy. They correspond to a non-existing Galois extension or a non-existing Galois group.
Galois Fields And Galois Teams
What’s a Galois extension, and what’s a Galois group? Fact is, the names are extra scary than their precise meanings are. Allow us to take into account the best instance.
$$
x^2+1in mathbb{Q}[x]
$$
This equation represents a parabola that doesn’t come nearer than ##1## to the ##x##-axis and has due to this fact no actual options for ##x^2+1=0.## We’d like the imaginary unit ##i## to unravel the equation. So if we add ##i## to the rational numbers, then we can remedy it. We write ##i^2 +1 = 0## and name ## i ## a zero, or root of the rational polynomial ##p(x)=x^2+1.## So
$$
mathbb{Q}[x]/(p(x))cong mathbb{Q}(i) cong mathbb{Q}+icdot mathbb{Q}.
$$
All the trick now’s to look at that there’s one other zero, particularly ## -i ##, and a mapping
$$
iota, : ,a+ icdot b longmapsto a- icdot b
$$
which we all know as conjugation has the property to repair rational numbers and map one root to the opposite. ##iota## generates a (multiplicatively written), so-called Galois group ##operatorname{Gal}(mathbb{Q}(i)/mathbb{Q}) cong mathbb{Z}_2= langle iota ,|,iota^2=1 rangle ,## the cyclic group with two components. The group our computer systems and mild switches are based mostly on. The important half and purpose for the notation are, that the automorphisms in that group don’t have an effect on the rational coefficients, and due to this fact don’t have an effect on the polynomial both. This precept leads us on to Galois concept as a result of it really works for any polynomial. Let’s have a look at a extra sophisticated polynomial, ##q(x)=x^3-3x-1.## It has no rational root, i.e. it’s known as irreducible over the rational numbers. However it has three actual roots. Allow us to name the foundation that’s closest to the origin ##alpha.## Then – observe that we don’t have to know the numerical worth of ##alpha, ## solely that ##alpha^3=3alpha +1##
$$
q(x)=(x-alpha )(x+alpha^2-2)(x-alpha^2+alpha +2)
$$
If we outline ##sigma (alpha ):=2-alpha ^2## then
start{align*}
sigma^2(alpha)&=2-(2-alpha^2)^2 = -alpha^4+4alpha^2-2 = alpha^2-alpha -2
sigma^3(alpha )&= (2-alpha^2)^2-(2-alpha^2)-2=alpha (3alpha +1)-3alpha ^2=alpha
finish{align*}
and ##operatorname{Gal}(mathbb{Q}(alpha )/mathbb{Q}) cong mathbb{Z}_3= langle sigma ,|,sigma^3=1 rangle ## is once more a cyclic group. If we have a look at the options to ##x^n-1=0## then ##operatorname{Gal}(mathbb{Q}(eta)/mathbb{Q})cong mathbb{Z}_n## for a ##n##-th root of unity, i.e. ##eta^n=1.## In fact, this isn’t all the time the case. If we take into account extra sophisticated polynomials, we are going to get teams of upper order that aren’t essentially cyclic.
A Galois extension of the rational numbers is any subject extension that arises from including roots of rational polynomials to the rational numbers irrespective of what number of roots, or what number of polynomials. This leads usually to a sequence of fields
$$
mathbb{Q} subset mathbb{Q}(alpha) subset mathbb{Q}(alpha,beta ) subset mathbb{Q}(alpha,beta ,gamma) subset ldots
$$
and a corresponding chain of Galois teams
$$
ldots supset underbrace{operatorname{Gal}(mathbb{Q}(alpha,beta,gamma)/mathbb{Q})supset operatorname{Gal}(mathbb{Q}(alpha,beta)/mathbb{Q})}_{{.,/,.;}cong;operatorname{Gal}(mathbb{Q}(alpha ,beta ,gamma )/mathbb{Q}(alpha ,beta ))}supset operatorname{Gal}(mathbb{Q}(alpha )/mathbb{Q})supset {1}
$$
The size of the sphere extensions are the indexes of the Galois teams.
Geometry and Galois Extensions
We need to describe what will be constructed with a compass and ruler, and nothing else. This has historic causes as a result of the traditional Greeks posed these three classical issues we talked about earlier with this restriction. We might get fully completely different issues if we allowed auxiliary instruments, e.g. an Archimedean spiral. So all we begin with are a compass, ruler, and a Cartesian coordinate system ##mathbb{Z}+imathbb{Z}## which will be constructed with them. Addition is then vector addition, and subtraction likewise. Multiplication wants the development
$$
x=acdot e^{ i alpha } , , ,y=bcdot e^{ i beta }Longrightarrow xcdot y= (acdot b)cdot e^{{i (alpha +beta )}}
$$
of angle addition and actual multiplication. The previous will be achieved on the unit circle, the latter with the intercept theorem. The division is solely the opposite approach round.
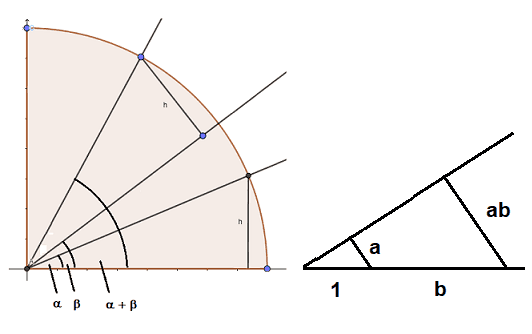The complicated numbers right here have solely been launched to visualise which constructions that should be achieved once we assemble rational numbers. The diagonal of squares permits us additionally the development of sq. roots of rational numbers. Therefore now we have proven the next theorem.
We are able to assemble a distance with a compass and ruler at any time when an answer to an issue is actual and will be calculated by rational operations and never essentially actual sq. roots from given distances …
This enough situation is important, too. See e.g. van der Waerden [1].
… and vice versa.
This theorem reads in mathematical phrases
Compass and ruler can assemble precisely any Galois extension of the rational numbers which have a level of an influence of two.
Squaring The Circle
Is it attainable to assemble a sq. with the identical space as a given circle?
We all know since 1882, Lindemann [2], now often known as Lindemann-Weierstraß theorem, that ##pi,## the Ludolph quantity named after the Sixteenth-century Dutch mathematician Ludolph van Ceulen, is transcendental. Because of this there isn’t a rational polynomial of any diploma such that ##pi## is a root. Therefore there isn’t a Galois extension of the rational numbers that features ##pi,## i.e. the space ##sqrt{pi}## is unimaginable to assemble with a compass and ruler.
Doubling The Dice
Is it attainable to assemble a dice with twice the quantity of a given dice?
If a given dice has a quantity ##1,## then we’re asking for a dice with a quantity ##2.## The facet size of such a dice could be ##sqrt[3]{2}.## The rational polynomial that has ##sqrt[3]{2}## as a root is ##x^3-2.## It has two extra irrational roots ##sqrt[3]{4};(-1pm isqrt{3}).## Because of this the Galois extension
$$
mathbb{Q}subset mathbb{Q}(sqrt[3]{2})
$$
is of diploma ##3## and therewith no energy of ##2.## Doubling the dice (with a compass and ruler) is unimaginable.
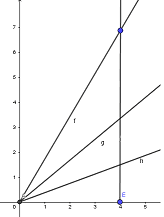
The Angle Trisection
Is it attainable to assemble a 3rd of an arbitrary given angle?
We are able to simply assemble, e.g., an angle of ##60°## which is a 3rd of ##180°.## It’s the slope of the straight ##y=sqrt{3} ,x,## the angle in an equilateral triangle, or of a hexagon. Thus, the query isn’t whether or not we will partition particular angles into their third components, however somewhat whether or not it may be achieved for any angle. Now, can we assemble the angles ##20°## and ##40°,## too? If we draw a circle of radius ##1## then discovering the angles is equal to discovering the heights
start{align*}
sin 60°&=sin (pi/3)=sqrt{3}/2approx 0.866
sin 40°&=sin (2pi/9)approx 0.643text{ vs. }2cdot 0.866 / 3 =0.577
sin 20°&=sin(pi/9)approx 0.342text{ vs. }0.866 / 3 =0.289
finish{align*}
It’s apparent, that we can not merely minimize the peak at ##60°## in three components with a purpose to get a 3rd of ##60°.## ##sqrt{3}/2## is not any downside since it’s the root of the quadratic rational polynomial ##x^2-3/4## which belongs to a Galois extension of diploma two. However are ##sin 20°## and ##sin 40°## even algebraic or are they transcendental? E.g.
$$
sin 20°=-dfrac{1}{2} (-1)^{7/18}((-1)^{2/9} – 1)
$$
Thankfully, it doesn’t play a task. Allow us to take into account the formulation
$$
cos(3alpha )=4cos^3(alpha )-3cos(alpha )
$$
In our instance, we get for ## x:=cos(20°)##
$$
0.5=cos(60°)=4cos^3(20°)-3cos(20°)=4x^3-3x
$$
The answer to this equation isn’t transcendental, nonetheless, it can’t be cut up into elements over the rational numbers. Its roots contain expressions with the cubic root of one thing, and cubic roots are of diploma three and due to this fact out of attain for our compass and ruler. ##20°## can’t be constructed.
Polynomials of 5-th Diploma or Greater
Fixing linear or quadratic integer polynomials is what we be taught in school
start{align*}
5x + 30 &= 0 Longrightarrow x=6
5x^2+30x+90&=0Longrightarrow x=-3pmsqrt{-9}=-3pm 3i
finish{align*}
Cubic and quartic equations will be solved by Cardano’s formulation (1545). Nevertheless, it’s disagreeable, doable however disagreeable. E.g. if the polynomial ##p(x)=ax^3+bx^2+cx+d## has precisely one intersection with the ##x##-axis, i.e. precisely one actual root, then ##p(x)=0## is solved by
start{align*}
x&=-dfrac{b}{3a}-dfrac{1}{3a}sqrt[3]{D+sqrt{D^2- (b^2-3ac)^3}}-dfrac{1}{3a}sqrt[3]{D-sqrt{D^2- (b^2-3ac)^3}}
finish{align*}
with ##D=b^3-dfrac{9}{2}abc+dfrac{27}{2}a^2nd.##
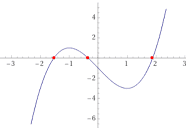
The theory of Abel-Ruffini states {that a} common polynomial equation of diploma 5 or larger can’t be solved by radicals, means, or root expressions. In fact, there are polynomials of diploma 5 or larger which can be solvable, e.g.
$$
0=x^5 – 15 x^4 + 85 x^3 – 225 x^2 + 274 x – 120=(x-1)(x-2)(x-3)(x-4)(x-5),
$$
however, e.g. ##x^5+x^2+1=0,## can solely be solved numerically. The primary proof of this theorem was printed by Ruffini in 1799. Nevertheless, his proof was patchy and largely ignored. An entire proof was given by Abel in 1824. However a deeper understanding of the matter can solely be achieved by Galois concept. Observe that we’re not restricted to Galois extensions of diploma ##2^n## because the compass and ruler are irrelevant for fixing polynomial equations. Nonetheless, we’re restricted to Galois extensions. Each root will be written with algebraic operations over rational numbers and root expressions ##sqrt[n]{, . ,}## means, that it is a component of a sure Galois extension of the rational numbers.
We’ve already noticed in two examples ##x^2+1## and ##x^3-3x-1##, that the weather of the Galois teams, that are automorphisms of the Galois fields that hold the bottom subject invariant, map roots to roots just like the complicated conjugation ##iota## and ##sigma ## in our examples did. They hop round on the set of roots, i.e. they generate finite permutation teams. And though now we have no restriction on the diploma of Galois extensions anymore, we nonetheless require the existence of these permutation teams that correspond to Galois extensions if we need to write the roots of rational polynomials with root expressions.
One can present that the Galois teams of such a polynomial equation should be solvable if the equation is solvable (by root expressions; e.g. [1].) Observe the coincidental naming! What’s a solvable group? It’s a group ##G## that permits a sequence of regular subgroups
$$
{1} underbrace{triangleleft}_{G_1} G_1 underbrace{triangleleft}_{G_2/G_1} G_2 underbrace{triangleleft}_{G_3/G_2} G_3
underbrace{triangleleft}_{G_4/G_3} G_4 underbrace{triangleleft}_{ldots}ldotsunderbrace{triangleleft}
_{G_n/G_{n-1}} G_n=G
$$
such that each one quotient teams ##G_k/G_{k-1} ## are abelian. All alternating teams ##A_n## are easy if ##ngeq 5.## Meaning they don’t have any non-trivial regular subgroups. This reduces the traditional chains of the permutation teams to
$$
{1}underbrace{triangleleft}_{A_n} A_n underbrace{triangleleft}_{S_n/A_ncong mathbb{Z}_2} S_n
$$
for ##ngeq 5.## Nevertheless, the alternating teams of upper orders are usually not abelian anymore
$$
(123)cdot (345)=(12345) neq (12453)=(345) cdot (123)
$$
and due to this fact not solvable. No solvable permutation teams imply no solvable polynomials and the theory together with the proofreads.
Theorem of Abel-Ruffini
Equations of the shape ##x^n+a_1x^{n-1}+ldots+a_n=0## can usually not be solved if ##ngeq 5.##
Proof: All alternating teams ##A_n## are easy if ##ngeq 5,## and particularly not solvable.##; sq.##
[ad_2]
