Numeral and Quantity Methods. Origin and Improvement
[ad_1]
A quantity is an summary idea used to compute or measure one thing.
A numeral is a logo representing a quantity.
A quantity system is a set of numbers sharing the identical traits.
A numeral system is a mixture of particular numerals.
Folks have been making an attempt to retailer and cross the data on as quickly as they discovered the right way to talk.
The primary makes an attempt to depict numbers have been executed utilizing the pictures of sticks or stones – largely to depend the variety of objects.
As civilization superior, the necessity to develop numeral and quantity programs that will enable folks to finish extra complicated mathematical operations grew. With the implementation of taxation programs, elevated commerce, evolving development wants, curiosity in sciences, mathematicians have been in search of extra environment friendly methods of representing numbers.
Quantity Bases and Quantity Teams
Counting as much as 10 (primarily based on the variety of fingers on one’s hand) ultimately grew to become not sufficient and other people had to think about a approach of representing bigger numbers utilizing symbols.
Thus, the quantity bases and quantity teams emerged.
10 was a preferred base (nevertheless, Babylonians, for instance, used base-sixty and Mayans used base-twenty), as a result of it was simple to depend on fingers and depend by 10s.
Different numbers have been additionally used to signify teams of numbers (a dozen, for instance).
The symbols representing ones and tens first appeared in Egypt and Mesopotamia round 3400-3000 BC.
Easy grouping numeral programs have been used to depict massive numbers and mathematical expressions involving a couple of arithmetic operation.
Egyptians repeated the symbols as much as 9, with a particular image for 10.
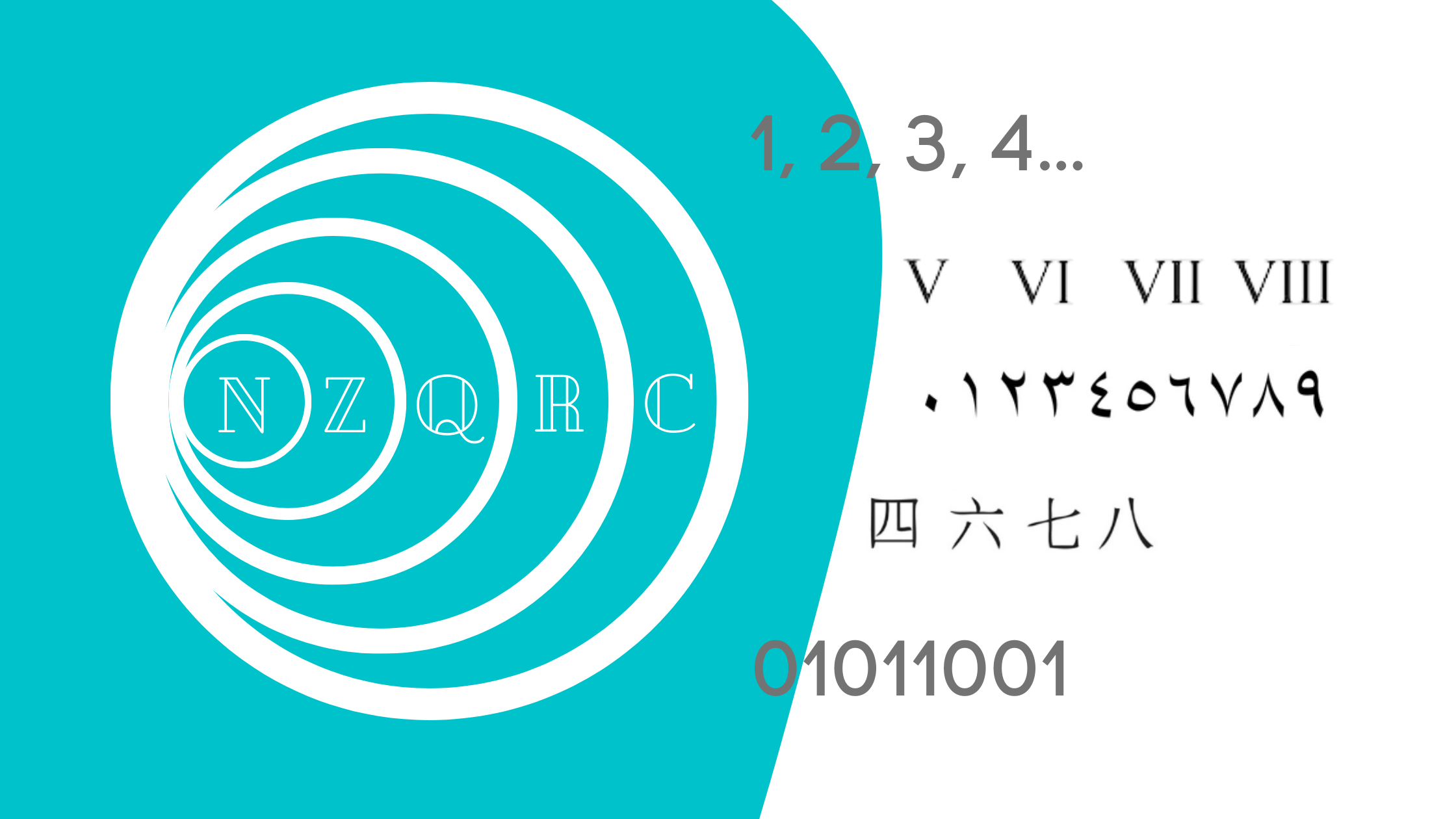
Greeks and Romans had an identical approach of representing massive numbers and performing arithmetic operations.
Roman numerals have been widespread for nearly 2000 years.

The Roman numerals system was a handy system primarily based on letters: I, V, X, L, C, D and M.
The system first emerged between 900 and 800 B.C and continues to be utilized in some contexts right now.
Trendy Numeral System
The decimal numeral system that we use right now originated in India and was additional developed in Persia.
The Chinese language system was additionally a decimal system, the place counting was primarily based on ten numerals represented by symbols. It had particular characters to signify ten, 100, a thousand, ten thousand, in addition to different multiples of ten.

The fashionable numerals system known as Hindu-Arabic: 1, 2, 3, 4, 5, 6, 7, 8, 9 and 0.
The system is positional, which signifies that the place of a logo determines the place worth of that image throughout the quantity (235 is 2 hundred + thirty + 5).
Round 1500 BC – 500, Indians have been actually keen on Astronomy and thus, the calculations concerned very massive numbers. They expressed these numbers utilizing a place-value notation, giving names for the powers of 10.
The complete system was first described exterior India in Al-Khwarizmi’s On the Calculation with Hindu Numerals ( in 825).
The earliest European manuscript, Codex Vigilanus, containing these numerals was written in Spain in 976. An Italian mathematician, Fibonacci, additional popularized the system in Europe.

Quantity Methods
Numbers are categorized into quantity programs primarily based on their traits and properties.
There are 5 important quantity programs that we use to categorise numbers:
- Pure Numbers
- Integers
- Rational Numbers
- Actual Numbers
- Advanced (Imaginary) Numbers
Pure numbers – constructive integers that we use to depend.
The image for the set of all pure numbers is
Integers – a mixture of a zero, unfavorable and constructive complete numbers. Zero is neither constructive nor unfavorable. Detrimental numbers are numbers which can be lower than zero. We use them to depict opposites, deficits, and so on.
The summary idea of unfavorable numbers was described round 100 B.C.. – 50 B.C. within the Chinese language ”9 Chapters on the Mathematical Artwork” (Jiu-zhang Suanshu) which supplied explanations on the right way to discover areas of figures the place crimson traces have been used for constructive coefficients and black have been used for unfavorable coefficients.
Greek mathematician Diophantus described integers and integer equations in his work Arithmetica.
The image for the set of all integers is (German Zahl, plural Zahlen – which means “numbers”).
Rational numbers – numbers that may be expressed as fractions with an integer numerator and a non-zero pure quantity denominator. The denominator can’t be 0 since we can not divide by 0. However a worth of the entire fraction can equal 0.
Fractions will be constructive and unfavorable.
Integers are a part of the set of all rational numbers, since each integer will be given as a fraction with a denominator 1.
Rational numbers may very well be discovered within the texts of Historical Egypt, describing the right way to convert fractions. Indian and Greek mathematicians studied rational numbers as a part of the quantity concept.
The image for the set of all rational numbers is (which means “quotient” – the end result of the division).
Irrational numbers are numbers that can’t be expressed as repeating, terminating decimals or as a ratio of two integers. Two particular examples of irrational numbers are numbers 𝚎 and 𝛑 .
The necessity for understanding and contemplating irrational numbers was established round 500 BC by a Greek mathematician Pythagoras.
These numbers shouldn’t have their very own set image.
Actual numbers – the entire rational and irrational numbers ( (-) – from unfavorable to constructive infinity). On a quantity line actual numbers replenish all of the area.
Within the seventeenth century, Rene Decartes launched the time period “actual” to explain roots of a polynomial (distinguishing them from imaginary numbers). Though with the event of Calculus actual numbers units and the idea of infinity have been extensively used, actual numbers have been for the primary time formally outlined in 1871 by Georg Cantor.
The image for the true numbers is
Advanced (imaginary) numbers outcome from taking a sq. root of a unfavorable quantity. The ensuing quantity is denoted by i, a logo assigned by Leonhard Euler.
The image for the true numbers is
Each previous set of numbers is a subset for the next quantity system.
Binary Quantity System
A Binary quantity system is the only of all positional programs and is extensively utilized in Laptop Science (computer systems use the binary quantity system to control and retailer all of their information together with numbers, phrases, movies, graphics, and music).
The bottom of the binary system is 2 and solely two numbers are used: 0 and 1.
Gottfried Leibniz, the co-creator of Calculus, first printed his invention of the binary system within the seventeenth century.
In a binary quantity system the primary 10 numbers can be represented as:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, and 1010
We are able to convert binary numbers into decimal numbers.
To transform 10101 from binary to decimal system we might do the next (a subscripts represents the bottom – 2 for binary and 10 for decimal):
Changing from binary to decimal, a binary quantity for can be
Additionally take a look at:
[ad_2]