
Parallel Programming on an NVIDIA GPU
[ad_1]
This text is the primary of a two-part sequence that presents two distinctly completely different approaches to parallel programming. Within the two articles, I take advantage of completely different approaches to unravel the identical drawback: discovering the best-fitting line (or regression line) for a set of factors.
The 2 completely different approaches to parallel programming introduced on this and the next Insights article use these applied sciences:
- Single-instruction multiple-thread (SIMT) programming is offered on the Nvidia® household of graphics processing items (GPUs). In SIMT programming, a single instruction is executed concurrently on tons of of microprocessors on a graphics card.
- Single-instruction a number of knowledge (SIMD) as offered on x64 processors from Intel® and AMD® (this text). In SIMD programming, a single instruction operates on extensive registers that may comprise vectors of numbers concurrently.
The main focus of this text is my try to train my laptop’s Nvidia card utilizing the GPU Computing Toolkit that Nvidia offers. The follow-on article, Parallel Programming on a CPU with AVX-512 | Physics Boards, makes use of Intel AVX-512 meeting directions and contains comparability occasions of the outcomes from each applications.
Introduction
Though I put in the Nvidia GPU Computing Toolkit and related samples about 5 years in the past, I didn’t do a lot with it, writing solely a small variety of easy applications. Extra not too long ago, I made a decision to take one other take a look at GPU programming, utilizing the newer graphics card on my extra highly effective laptop.
After I downloaded a more recent model of the GPU Computing Toolkit (ver. 10.0 – newer variations exist) and acquired all the pieces arrange, I proceeded to construct a number of the many samples offered on this toolkit. I then determined to attempt my talent at placing collectively the instance program that’s described on this article.
Regression line calculations
Given a set of factors (Xi, Yi), the place i ranges from 1 to N, the slope m and y-intercept b of the regression line could be discovered from the next formulation.
$$m = frac{N left(sum_{i = 1}^N X_iY_i proper)~ -~ left(sum_{i = 1}^N X_i proper) left(sum_{i = 1}^N Y_i proper)}{Nleft(sum_{i = 1}^N X_i^2right) – left(sum_{i = 1}^N X_iright)^2 }$$
$$b = frac{sum_{i = 1}^N Y_i – sum_{i = 1}^N X_i} N$$
As you possibly can see from these formulation, there are plenty of calculations that have to be carried out. This system should calculate the sum of the x coordinates and the sum of the y coordinates. It should additionally calculate the sum of the squares of the x coordinates and the sum of the term-by-term xy merchandise. For the latter two sums, it’s handy to create two new vectors. The primary vector consists of the term-by-term merchandise of the x coordinates with themselves. The second consists of the term-by-term product of the x- and y-coordinates.
Disclaimer
Though this system I’m presenting right here makes use of the GPU to calculate the term-by-term vector merchandise ##< X_i Y_i>## and ##<X_i^2>## , it does not use the GPU to calculate the 4 sums. It seems that this can be a extra difficult drawback to deal with. Though the NVidia Toolkit offers samples of summing the weather of a vector, these examples are thought-about superior matters. For that cause, my code doesn’t use the GPU to calculate these sums.
Primary phrases
- thread – the essential unit of computation. Every core is able to operating one thread. Threads are organized into blocks, which could be one-dimensional, two-dimensional, or three-dimensional. For that reason, a thread index, threadIdx, can have one, two, or three elements, relying on how the blocks are laid out. The three elements are threadIdx.x, threadIdx.y, and threadIdx.z. Thread indexes that aren’t used have default values of 1.
- block – a set of threads. As a result of blocks could be organized into one-dimensional, two-dimensional, or three-dimensional preparations, a person block could be recognized by a number of block indexes: blockIdx.x, blockIdx.y, or blockIdx.z. Block indexes that aren’t used have default values of 1. All vectors in my program are one-dimensional, so threadIdx.y, threadIdx.z, blockIdx.y, and blockIdx.z aren’t related. A program working with picture knowledge would doubtless use a two-dimensional grid, and would subsequently use a few of these different builtin variables.
- grid – a set of blocks, with the blocks containing threads.
The CUDA kernel
To entry the NVidia GPU structure, a programmer makes use of the API offered within the NVidia GPU Toolkit to jot down a CUDA (Compute Unified Gadget Structure) program. Such a program will comprise at the least one CUDA kernel, NVidia’s time period for a per-thread perform that runs on one of many GPU’s cores. For the kernel proven beneath, every core will multiply the i-th components of two vectors, and retailer the consequence within the corresponding ingredient of a 3rd vector. The NVidia GPU I’m operating has 1,024 cores, it ought to make quick work of multiplying the weather of two vectors of pretty excessive dimension.
__global__ void
vectorMult(double *C, const double * A, const double * B, int numElements)
{
int i = blockDim.x * blockIdx.x + threadIdx.x;
if (i < numElements)
{
C[i] = A[i] * B[i];
}
}
When this kernel runs, every of probably 1,024 streaming multiprocessors (SMs) multiplies the values from two enter vectors, and shops the product as an output worth in a 3rd vector. Determine 1 exhibits these actions.
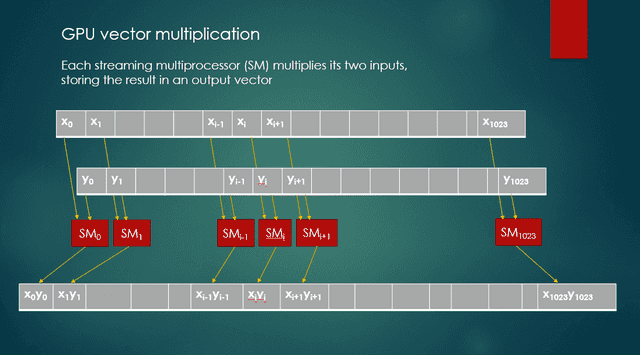
Fig. 1 GPU vector multiplication
vectorMult kernel particulars
The __global__ key phrase is a CUDA extension that signifies a perform is a kernel, and is meant to run on the GPU. A kernel perform’s return sort have to be void.
The perform header signifies that this perform takes 4 parameters. So as, these parameters are:
- a pointer to the output vector,
- a pointer to the primary enter vector,
- a pointer to the second enter vector,
- the variety of components in every of the three vectors.
The variable i establishes the connection between a selected thread and the corresponding index of the 2 enter vectors and the output vector. For this connection, this system has to establish a selected block inside the grid, in addition to the thread inside that block. For my program, every enter vector accommodates 262,144 double values. This quantity occurs to be 512 X 512, or ##2^{18}##. If I select a block measurement of 256 (that means 256 threads per block), there can be 1024 blocks within the grid. A block measurement of 256 in a one-dimensional association signifies that blockDim.x is 256.
For instance within the code pattern above, to entry thread 2, in block 3, blockDim.x is 256, blockIdx.x is 3, and threadIdx.x is 2. In Determine 2, block 3 and thread 2 are proven. The index for the enter and output vectors is calculated as 256 * 3 + 2, or 770. Thread 2 of block 3 is the ##770^{th}## thread of the grid. Remember the fact that a GPU can carry out tons of of a lot of these per-thread computations concurrently.
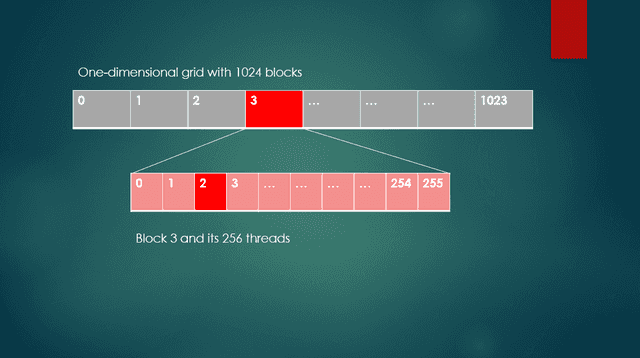
Fig. 2 One dimensional grid with a block and threads
The CUDA program
To make use of the capabilities of a GPU, a program should carry out the next steps.
- Allocate reminiscence on the host.
- Initialize enter vector knowledge.
- Allocate reminiscence on the system.
- Copy knowledge from the host to the system.
- Arrange parameters for a name to the kernel, together with the variety of blocks within the grid, and the variety of threads per block, in addition to the parameters of the kernel perform itself.
- Name the kernel.
- Copy output knowledge from the system again to the host.
- Free system reminiscence and host reminiscence.
Every of those steps is mentioned within the subsequent sections.
Allocate host reminiscence
This system allocates reminiscence on the host by utilizing the C customary library perform, malloc. This needs to be acquainted to anybody with expertise in C programming. All through the code, an h_ prefix denotes a variable in host reminiscence; a d_ prefix denotes a variable in system reminiscence on the GPU.
int numElements = 512 * 512; // = 262144, or 2^18 size_t measurement = numElements * sizeof(double); double *h_X = (double *)malloc(measurement); double *h_Y = (double *)malloc(measurement); double *h_XY = (double *)malloc(measurement); double *h_XX = (double *)malloc(measurement);
Initialize enter knowledge
For the sake of simplicity in addition to a verify on program accuracy, the info within the enter vectors are factors that each one lie on the road ##y = 1.0x + 0.5##. The loop beneath initializes the h_X and h_Y vectors with the coordinates of those factors. The loop beneath is “unrolled” with every loop iteration producing 4 units of factors on the road.
const double slope = 1.0;
const double y_int = 0.5;
// Fill the host-side vectors h_X and h_Y with knowledge factors.
for (int i = 0; i < numElements; i += 4)
{
h_X[i] = slope * i;
h_Y[i] = h_X[i] + y_int;
h_X[i + 1] = slope * i;
h_Y[i + 1] = h_X[i + 1] + y_int;
h_X[i + 2] = slope * (i + 2);
h_Y[i + 2] = h_X[i + 2] + y_int;
h_X[i + 3] = slope * (i + 3);
h_Y[i + 3] = h_X[i + 3] + y_int;
}
Allocate system reminiscence
This system allocates reminiscence on the system by utilizing the CUDA cudaMalloc perform. The primary parameter of cudaMalloc is a pointer to a pointer to the kind of ingredient within the vector, solid as sort void**. The second parameter is the variety of bytes to allocate. The cudaMalloc perform returns cudaSuccess if reminiscence was efficiently allotted. Some other return worth signifies that an error occurred.
double *d_X = NULL; err = cudaMalloc((void **)&d_X, measurement);
The code for allocating reminiscence for d_Y is sort of an identical.
Copy knowledge from host to system
To repeat knowledge from host (CPU) to system (GPU) or from system to host, use the CUDA cudaMemcpy perform. The primary parameter is a pointer to the vacation spot vector, and the second parameter is a pointer to the supply vector. The third parameter is the variety of bytes to repeat, and the fourth parameter signifies whether or not the copy is from host to host, host to system, system to host, or system to system.
err = cudaMemcpy(d_X, h_X, measurement, cudaMemcpyHostToDevice);
This perform returns cudaSuccess if the info was efficiently copied. Related code copies the values in h_Y to d_Y on the system.
Arrange parameters for the decision to the kernel
Earlier than calling a kernel, this system should decide the variety of threads per block and the quantity blocks in a grid. Within the following instance, the variety of blocks per grid is successfully the variety of components divided by 256. The marginally extra difficult calculation guards in opposition to grid sizes that aren’t a a number of of the block measurement.
int threadsPerBlock = 256; int blocksPerGrid = (numElements + threadsPerBlock - 1) / threadsPerBlock;
Name the kernel
The NVidia Toolkit contains its personal compiler that extends C or C++ syntax for calling kernels. The syntax makes use of a pair of triple angle brackets (<<< >>>) that comply with the identify of the kernel. These angle bracket pairs comprise two parameters — the variety of blocks within the grid, and the variety of threads per block. A 3rd parameter is elective.
The parameters of the vectorMult kernel proven within the following instance include, respectively, the vacation spot vector’s tackle, the addresses of the 2 enter vectors, and the variety of components of every vector. This kernel name passes management to the GPU. The CUDA system software program handles all the main points concerned in scheduling the person threads operating within the processors of the GPU.
vectorMult <<<blocksPerGrid, threadsPerBlock >>> (d_XY, d_X, d_Y, numElements);
Copy output knowledge again to the host
Copying knowledge from the system again to the host is the reverse of copying knowledge from the host to the system. As earlier than, the primary parameter is a pointer to the vacation spot vector, and the second parameter is a pointer to the supply vector. The third parameter, cudaMemcpyDeviceToHost, signifies that knowledge can be copied from the system (GPU) to the host. If the reminiscence copy is profitable, cudaMemcpy returns cudaSuccess. The code beneath copies the values in d_XY on the system to the vector h_XY in host reminiscence. Related code copies the values in d_XX on the system to the vector h_XX in host reminiscence.
err = cudaMemcpy(h_XY, d_XY, measurement, cudaMemcpyDeviceToHost);
Free system and host reminiscence
The primary line beneath frees the reminiscence allotted for the d_X vector, utilizing the cudaFree perform. As is the case with most of the CUDA capabilities, it returns a worth that signifies whether or not the operation was profitable. Any worth aside from cudaSuccess signifies that an error occurred. To free the host vector, use the C reminiscence deallocation perform, free. Related code deallocates the reminiscence utilized by the opposite system and host vectors.
err = cudaFree(d_X); free(h_X);
Program output
The final 4 traces present that the computed values for slope and y-intercept agree with people who had been used to generate the factors on the road, which confirms that the calculations are right.
[Linear regression of 262144 points] CUDA kernel launch with 1024 blocks of 256 threads Sum of x: 34359541760.000000 Sum of y: 34359672832.000000 Sum of xy: 6004765143567284.000000 Sum of x^2: 6004747963793408.000000 Processed 262144 factors Predicted worth of m: 1.000000 Computed worth of m: 1.0000000000 Predicted worth of b: 0.500000 Computed worth of b: 0.5000000000
Full code
For the sake of brevity, I haven’t included the entire supply code right here on this article. In case your curiosity is piqued, you could find the supply code for this text, RegressionLine2.cu right here: https://github.com/Mark44-AVX/CUDA-vs.-AVX-512.
[ad_2]






