Space System – Checklist of Essential Formulation
[ad_1]
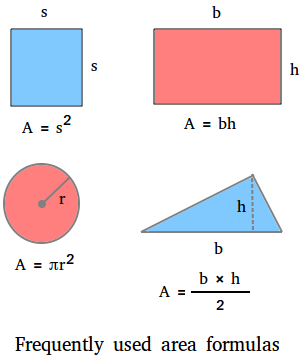
The world formulation is used to seek out the variety of sq. models a polygon encloses. The determine beneath reveals some space formulation which are ceaselessly used within the classroom or within the real-world.
Space of a sq.
The world of a sq. is the sq. of the size of 1 aspect. Let s be the size of 1 aspect.
A = s2 = s × s
Space of a rectangle
The world of a rectangle is the product of its base and peak.
Let b = base and let h = peak
A = b × h = bh
For a rectangle, “size” and “width” can be used as a substitute of “base” and “peak”
The world of a rectangle can be the product of its size and width
A = size × width
Space of a circle
The world of a circle is the product of pi and the sq. of the radius of the circle.
Let r be the radius of the circle and let pi = π = 3.14
A = πr2
Please see the lesson about space of a circle to get a deeper data.
Space of a triangle
The world of a triangle is half the product of the bottom of the triangle and its peak.
Let b = base and let h = peak
Space = (b × h)/2
Space of a parallelogram
The world of a parallelogram is the product of its base and peak.
Let b = base and let h = peak
A = b × h = bh
Please see the lesson about parallelogram to study extra.
Space of a rhombus
The world of a rhombus / space of a kite is half the product of the lengths of its diagonals.
Let d1 be the size of the primary diagonal and d2 the size of the second diagonal.
A = (d1 × d2)/2
Space of a trapezoid
The world of a trapezoid is half the product of the peak and the sum of the bases.
Let b1 be the size of the primary base, b2 the size of the second base, and let h be the peak of the trapezoid.
A = [h(b1 + b2)]/2
Please see the lesson about space of a trapezoid to study extra.
Space of an ellipse
The world of the ellipse is the product of π, the size of the semi-major axis, and the size of the semi-minor axis.
Let a be the size of the semi-major axis and b the size of the semi-minor axis.
A = πab
The semi-major axis can also be known as main radius and the semi-minor axis known as minor radius.
Let r1 be the size of the semi-major axis and r2 the size of the semi-minor axis.
The world can also be equal to πr1r2
A few instance exhibiting use the realm formulation
Instance #1
What’s the space of an oblong yard whose size and breadth are 50 toes and 40 toes respectively?
Answer:
Size of the yard = 50 ft
Breadth of the yard = 40 ft
Space of the yard = size × breadth
Space of the yard = 50 ft × 40 ft
Space of the yard = 2000 sq. toes = 2000 ft2
Instance #2
The lengths of the adjoining sides of a parallelogram are 12 cm and 15 cm. The peak equivalent to the 12-cm base is 6 cm. Discover the peak equivalent to the 15-cm base.
Answer:
A = b × h = 12 × 6 = 72 cm2
For the reason that space continues to be the identical, we are able to use it to seek out the peak equivalent to the 15 cm base.
A = b × h
Substitute 72 for A and 15 for b.
72 = 15 × h
Divide either side of the equation by 15
72/15 = (15/15) × h
4.8 = h
The peak equivalent to the 15 cm base is 4.8 cm.
Instance #3
The diameter of a circle is 9. What’s the space of the circle?
Answer:
For the reason that radius is half the diameter, r = 9/2 = 4.5
A = πr2
A = 3.14(4.5)2
A = 3.14(20.25)
A = 63.585
[ad_2]
You may also like
Idea of Sample | Related Patterns in Arithmetic
