The Historical past and Significance of the Riemann Speculation

Riemann Speculation Historical past

The historical past of the Riemann speculation could also be thought of to begin with the primary point out of prime numbers within the Rhind Mathematical Papyrus round 1550 BC. It actually started with the primary treatise of prime numbers in Euclid’s Parts within the third century BC. It got here to a – hopefully momentary – finish on the eighth of August 1900 on the listing of Hilbert’s well-known issues. And primes are the rationale why we’re greater than ever within the query of whether or not ERH holds or not. For e.g. the RSA encryption algorithm (Rivest-Shamir-Adleman, 1977) depends on the complexity of the factorization drawback FP, that it’s NP-hard. FP might be neither NP-complete nor in P however we have no idea for positive. Early factorization algorithms that ran in an affordable time needed to assume the prolonged Riemann speculation (Lenstra, 1988, [1]). So what do prime numbers have in frequent with the Riemann speculation which is a couple of perform outlined as a Dirichlet sequence?
$$
zeta(s)=sum_{n=1}^infty dfrac{1}{n^s}
$$
One has to confess that what we name prime quantity concept as we speak originated within the nineteenth century when Dirichlet started in 1837 to use evaluation to quantity concept. There’s a massive hole between Euclid and Euler who revealed a brand new proof for the infinite variety of primes in 1737.

Prime Numbers

A brief reply could be that
$$
zeta(s)=sum_{n=1}^infty dfrac{1}{n^s}=prod_{ptext{ prime}}dfrac{1}{1-{p}^{-s}}.
$$
That is simple to show [5] however falls a bit in need of the connection between prime numbers and the Riemann speculation. E.g. the fundamental concept for our instance of why FP will be solved rapidly beneath the idea of ERH is, that ERH implies the existence of comparatively small primes which then will be discovered by quick algorithms. (See the theorems of Ankeney/Montgomery/Bach, Miller, Bach [10] and the references therein.)

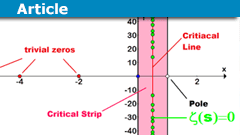
Let ##1/2 leq theta leq 1.## Then

$$massive{operatorname{RH}(theta), : ,zeta(s) textual content{ has no zeros in }{mathfrak{R}(s)>theta}}$$

is one other generalization of the Riemann speculation. The unique Riemann speculation is thus ##operatorname{RH}(1/2)## and we all know there aren’t any zeros of the zeta-function in ##{mathfrak{R}(s)>1}##. So ##operatorname{RH}(1)## is true, however no proof is thought for values of ##theta## under. We do know ([7],[8],[9]) that
$$
massive{operatorname{RH}(theta)quad Longleftrightarrowquad pi(x)=operatorname{Li}(x) + Oleft(x^{theta +varepsilon }proper)textual content{ for all }varepsilon >0}
$$
the place ##operatorname{Li}(x)=displaystyle{int_2^x dfrac{dt}{log t}}## is the integral logarithm and ##pi(x)=left|{pin mathbb{P},|,pleq x}proper|## the prime quantity perform (graphic from [2]). Therefore ERH is related to the query: The place are the primes?

 

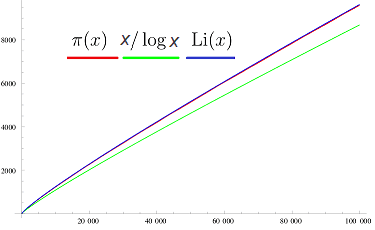
The prime quantity theorem
$$
lim_{x to infty}dfrac{pi(x)}{dfrac{x}{log(x)}}=1
$$
was first conjectured by Gauß in 1792, nevertheless, confirmed by Hadamard and de la Vallée-Poussin independently 100 years later in 1896. Their proofs have been of perform theoretical nature and relied on the relation of primes to the Riemannian ##zeta##-function which was first thought of by Euler within the 18th century.

One other fascinating equal formulation of ##operatorname{RH}(theta)## is the next: Let ##a_{even}## be the variety of integers under ##x>0## which might be a product of a good variety of primes, and ##a_{odd}## be the variety of integers under ##x>0## that may be a product of an odd variety of primes, then
$$
massive{operatorname{RH}(theta)quad Longleftrightarrowquad a_{even}(x)-a_{odd}(x) = Oleft(x^{theta +varepsilon }proper)textual content{ for all }varepsilon >0.}
$$
These two equations present that the Riemann speculation shouldn’t be solely a couple of Dirichlet sequence, or the security of some encryption algorithms. It’s why I stated all of it started with the notion of prime numbers. We merely need to understand how prime numbers are distributed. Historical past reveals that we’re fascinated by prime numbers. The Riemann speculation ##operatorname{RH}(1/2)## is in the meantime checked for the primary ##10,000,000,000,000## zeros of the ##zeta##-function [11], i.e. some other outcome than its reality could be greater than stunning. Ultimately, we will examine as many zeros as our computer systems can deal with, it should by no means be a proof. Nevertheless, these outcomes above marked an enormous step within the concept of prime numbers. It wasn’t lengthy earlier than when Euler (1707 – 1783) wrote:

“Mathematicians have hitherto strove in useless to find any order within the sequence of prime numbers, and one is inclined to imagine that this can be a thriller which the human thoughts won’t ever fathom. To persuade oneself of this, one want solely look on the prime quantity tables, which some have taken the difficulty to increase to 100,000, and one will at first discover that there isn’t any order, no rule to be noticed.” [12]

Early Glory

Riemann’s conjecture was solely by the way talked about by Riemann himself, and never explicitly recognized as an necessary drawback. Riemann wrote in regards to the zeros:

“In truth, one finds many roots inside these limits, and it is rather possible that each one the roots are there. After all, a rigorous proof of this could be fascinating; nevertheless, after just a few unsuccessful makes an attempt, I’ve left the seek for it apart in the meanwhile, because it appears pointless for the aim of my investigation.”

Nonetheless, he has confirmed that there are infinitely many roots ##s## of the ##zeta##-function with ##mathfrak{R}(s)=1/2## and that virtually all roots are shut to the essential line. Siegel has found these proofs in 1935 when he investigated Riemann’s property. Riemann by no means revealed them. It was Hardy 1914 who first revealed a proof that there are infinitely many zeros on the essential line. Somewhat later 1921, Hardy and Littlewood proved that there’s a fixed ##A>0## such that there are greater than ##AT## zeros with actual half ##1/2## whose (absolute) imaginary half is smaller than ##T.## It follows that there’s a non-zero proportion ##B## of zeros on the essential line. Levinson confirmed in 1974 that ##B>1/3.##

It isn’t fairly clear whether or not Hardy believed in God or was simply superstitious. Nevertheless, in any case, he believed God will do the whole lot to make his life powerful and complex. Sooner or later, he was on a journey again residence from a gathering with Harald Bohr (Niels Bohr’s brother) in Copenhagen. He needed to take a ship and the boat he received didn’t look very trustful. Usually, he thought, why me?
So he despatched a postcard earlier than boarding to Bohr claiming he has discovered the proof of Riemann’s speculation. When requested afterward, why, he replied: Nicely, if the ship sank the proof would have been misplaced however I might have grow to be probably the most well-known mathematician of my technology. God received’t enable this to occur. That manner I solely needed to write Bohr one other postcard through which I revealed to have made a mistake.

This anecdote and information show how well-known the Riemann speculation was already at the start of the final century regardless of Riemann’s indifference to the issue that since carries his identify.

Hilbert had been invited to offer a lecture on the second worldwide congress of mathematicians in August 1900 in Paris. He determined to not give a lecture through which he would report and respect what had been achieved in arithmetic to this point, nor to reply to Henri Poincaré’s lecture on the first worldwide congress of mathematicians in 1897 on the connection between arithmetic and physics. As a substitute, his lecture was meant to supply a type of programmatic outlook on future arithmetic within the coming century. This goal is expressed in his introductory phrases:

“Who amongst us wouldn’t prefer to carry the veil that hides the long run, to take a look on the forthcoming advances of our science and into the mysteries of its growth in the course of the centuries to come back! What specific objectives will or not it’s that the main mathematical minds of generations to come back will aspire to? What new strategies and new information will the brand new centuries uncover within the huge and wealthy subject of mathematical thought?”

He, due to this fact, took the congress as a chance to compile a thematically various listing of unsolved mathematical issues. As early as December 1899 he started to consider the topic. Initially of the brand new yr, he then requested his shut buddies Hermann Minkowski and Adolf Hurwitz for options as to which areas a corresponding lecture ought to cowl; each learn the manuscript and commented on it earlier than the lecture. Nevertheless, Hilbert solely lastly wrote down his listing instantly earlier than the congress – which is why it doesn’t but seem within the official congress program. The lecture was initially speculated to be given on the opening, however Hilbert was nonetheless engaged on it on the time. Now they’re referred to as Hilbert’s 23 issues. There was discovered a twenty fourth in his property: “How can the simplicity of a mathematical proof be measured, and the way can its minimal be discovered?”, however the official depend is 23. They’re partially very particular like the primary one: “Show the continuum speculation.” even when clearly not essentially solvable, or very imprecise just like the sixth one: “Mathematical therapy of the axioms of physics.” Right here we have an interest within the eighth: Show the Riemann speculation, the Goldbach conjecture, and the dual prime conjecture. [3]

“Not too long ago, important advances have been made within the concept of the distribution of prime numbers by Hadamard, de La Vallee-Poussin, V. Mangoldt, and others. Nevertheless, in an effort to utterly clear up the issues posed by Riemann’s treatise ‘On the Variety of Primes Under a Given Dimension’, it’s nonetheless essential to show the correctness of Riemann’s extraordinarily necessary declare that the zeros of the perform ##zeta(s)##, which is outlined by the sequence ##zeta (s)=1+frac{1}{2^{s}}+frac{1}{3^{s}}+cdots ##, all have the actual parts ##1/2## if one disregards the well-known damaging integer zeros. As quickly as this proof is profitable, the additional job could be to look at the Riemann infinite sequence for the variety of primes extra exactly and particularly to resolve whether or not the distinction between the variety of primes under a magnitude and the integral logarithm of ##x## turns into the truth is no greater than the ##tfrac{1}{2}##th order in ##x## at infinity, and additional, whether or not these from the primary advanced zeros of the perform ##zeta (s)## dependent phrases of Riemann’s formulation actually trigger the native compression of the prime numbers, which one observed when counting the prime numbers.” [13]

Sure, language was a unique one a century in the past. Hilbert himself categorised the Riemann speculation as more easy than, for instance, the Fermat drawback: in a lecture in 1919 he expressed the hope {that a} proof could be present in his lifetime, within the case of the Fermat conjecture maybe within the lifetime of the youngest listeners; he thought of the transcendence proofs in his seventh drawback to be probably the most troublesome – an issue that was solved within the Thirties by Gelfond and Theodor Schneider. The Fermat drawback was solved in 1995 by Andrew Wiles and Richard Taylor as a part of their proof of the modularity theorem. A proof that’s not solely slightly lengthy but in addition slightly technical and complex, so the comparability with the Riemann speculation is presumably not as far-fetched as it might sound.

“If I have been to awaken after having slept for a thousand years, my first query could be: Has the Riemann speculation been confirmed?” (David Hilbert) [6]

Randomness

Let’s summarize the central restrict theorem of likelihood concept by contemplating a good coin toss and we pay +1 for heads and money in -1 for tails. The well-known gambler’s fallacy is to imagine that after an extended straight of heads a tail would grow to be extra probably. That is fallacious as a result of randomness has no reminiscence. Likelihood is nonetheless fifty-fifty. Even our general acquire or loss ##L(n)## after ##n## tosses isn’t zero. It’s as unlikely that there can be precisely the identical variety of heads as there are tails as it’s that each one tosses could be heads. Nevertheless, it may be confirmed that the likelihood distribution of ##L(n)## converges pointwise to a traditional distribution, in our case the usual regular distribution which is the assertion of the central restrict theorem.

We have now really already seen the connection between the Riemann speculation and randomness
$$
operatorname{RH}(theta)quad Longleftrightarrowquad a_{even}(n)-a_{odd}(n) = Oleft(n^{theta +varepsilon }proper)textual content{ for all }varepsilon >0.
$$
Allow us to take into account the Liouville perform ##lambda (n)=(-1)^{#textual content{ prime elements of }n}## and do not forget that ##a_{even/odd}(n)## counted the variety of integers under ##n## which might be a product of a good/odd variety of primes. Then
$$
L(n)=sum_{ok=1}^n lambda (ok)= a_{even}-a_{odd}
$$
and the central restrict theorem says
$$
lim_{n to infty}dfrac{L(n)}{n^{varepsilon +1/2}}=0 textual content{ for all }varepsilon >0 Leftrightarrow L(n)=O(n^{varepsilon +1/2})
Leftrightarrow RH(1/2)$$
Which means the pseudo-randomness of the distribution of prime numbers is sort of impartial and an identical, i.e. actually random. It appears, Euler was proper as soon as extra.

Quantity Concept

We already talked about the fascination with prime numbers and their central that means in quantity concept. It’s no coincidence that there are three well-known issues listed beneath Hilbert’s eighth drawback:

1. Riemann Speculation
   ##a_{even}(n)-a_{odd}(n)=O(n^{varepsilon +1/2})##
2. Goldbach’s Conjecture
   Each even integer better than ##2## is the sum of two primes.
3. Twin Prime Conjecture
   There are infinitely many pairs ##(p,p+2)## of prime numbers ##p.##

Neither of those conjectures are confirmed though they’ve been examined for extremely massive quantities of numbers computationally. All of them should do with prime numbers. An integer ##p## is prime, if and provided that ## (p-1)!equiv -1 {pmod p}## (Wilson’s theorem), and a pair ##(p,p+2)## is a pair of primes, if and provided that ##4cdot ((p-1)!+1)+p equiv 0 {pmod {pcdot (p+2)}}## (Clement’s theorem).

Goldbach’s conjecture or the robust Goldbach conjecture has a weaker model: Each odd quantity better than ##5## is the sum of three primes. Since ##3## is prime and ##2n+1=2n-2+3=p+q+3,## the robust model implies the weaker, which has been partially solved. On one hand, is it true in case the prolonged Riemann speculation holds, and however, it holds for sufficiently massive numbers. If ##R(n)## is the variety of representations of ##n## because the sum of three prime numbers, then (Vinogradov’s theorem)
$$
R(n)=dfrac{n^2}{2(log n)^3}underbrace{left(prod_{pmid n}left(1-dfrac{1}{(p-1)^2}proper)proper)left(prod_{pnmid n}left(1+dfrac{1}{(p-1)^3}proper)proper)}_{=:G(n)}+Oleft(dfrac{n^2}{(log n)^4}proper)
$$
and it may be proven that ##G(2n)=0,## ##G(2n-1)geq 1,## and ##G(2n-1)## is asymptotically of order ##O(1),## therefore ##R(2n-1)>0## for sufficiently massive ##n.##

Physics

There have been fairly just a few makes an attempt to deal with the issue by bodily strategies, particularly these days. That is fairly stunning since arithmetic is a deductive science and physics a descriptive science. One can examine the outcomes of theoretical fashions in a bodily world, however how ought to real-world observations contribute to a mathematical conjecture? The origin of such a connection, nevertheless, isn’t fairly new. David Hilbert and Pólya György had already observed that the Riemann speculation would comply with if the zeros have been eigenvalues of an operator ##({tfrac{1}{ 2}}+iT)## the place ##T## is a Hermitian (i.e. self-adjoint) operator, which due to this fact has solely actual eigenvalues, much like the Hamiltonian operators in quantum mechanics. Additional concerns on this route find yourself within the concept of quantum chaos. Different connections have been drawn to statistical mechanics [3], or one-dimensional quasi-crystals [15]. We even had a customer on Physics Boards who tried to entry it by way of the hydrogen atom. All these ideas are primarily based on parallels between the Riemann speculation and likelihood distributions and are sometimes as a result of similarities in formulation.

Cryptology

Along with quite a few functions in lots of areas of arithmetic, the Riemann Speculation can also be of curiosity in cryptology. For instance, the RSA cryptosystem makes use of massive prime numbers to assemble each private and non-private keys. Its safety is predicated on the truth that standard computer systems don’t but have an environment friendly algorithm for dividing a quantity into its prime elements, i.e. to resolve FP. The idea behind RSA requires solely outcomes from elementary quantity concept. In 1976, once more primarily based on easy quantity concept and utilizing Fermat’s little theorem, Miller developed a deterministic primality check that works assuming the prolonged Riemann Speculation [16]. In 1980, Michael O. Rabin used Miller’s outcomes to develop a probabilistic check that labored independently of the prolonged Riemann speculation [17]. Via the work of Bach in 1990, this so-called Miller-Rabin check will be transformed right into a deterministic check that runs with the velocity ##O(log(n)^{2})##, once more assuming the prolonged Riemann Speculation [10]. All of the connections between the Riemann speculation and cryptology are at their core as a result of its that means for the distribution of prime numbers.