Venn Diagram Phrase Issues

The Venn diagram phrase issues on this lesson will present you use Venn diagrams with 2 circles to unravel issues involving counting. 

Venn diagram phrase issues with two circles

Phrase drawback #1

A survey was carried out in a neighborhood with 128 households. The survey revealed the next data.

• 106 of the households have a bank card
• 73 of the households try to repay a automobile mortgage
• 61 of the households have each a bank card and a automobile mortgage

Reply the next questions:

1. What number of households have solely a bank card?

2. What number of households have solely a automobile mortgage?

3. What number of households have neither a bank card nor a automobile mortgage?

4. What number of households shouldn’t have a bank card?

5. What number of households shouldn’t have a automobile mortgage?

6. What number of households have a bank card or a automobile mortgage?

• Let C be households with a bank card
• Let L be households with a automobile mortgage
• Let S be the entire variety of households

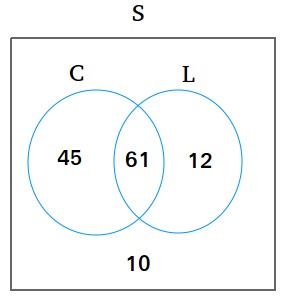
The Venn diagram above can be utilized to reply all these questions. 

Resolution

The expression, “solely a bank card” implies that it’s only in C. Any quantity in L can’t be included.

1. The variety of households with solely a bank card is 45. Don’t add 61 to 45 since 61 is in L.

2. The variety of households with solely a automobile mortgage is 12. 

3. The variety of households with neither a bank card nor a automobile mortgage is 10. 10 is just not in C nor in L.

4. The quantity households with out a bank card is discovered by including every thing that’s not in C.

12 + 10 = 22

5. The quantity households with out a automobile mortgage is discovered by including every thing that’s not in L.

45 + 10 = 55

6. The variety of households with a bank card or a automobile mortgage is discovered by including something in C solely, in L solely and within the intersection of C and L?

45 + 61 + 12 = 118

Phrase drawback #2

A survey carried out in a college with 150 college students revealed the next data:

• 78 college students are enrolled in swimming class
• 85 college students are enrolled in basketball class
• 25 are enrolled in each swimming and basketball class

Reply the next questions:

1. What number of college students are enrolled solely in swimming class?

2. What number of college students are enrolled solely in basketball class?

3. What number of college students are neither enrolled in swimming class nor basketball class?

4. What number of college students should not enrolled in swimming class?

5. What number of college students should not enrolled in basketball class?

6. What number of college students are enrolled in swimming class or basketball class?

• Let S be college students enrolled in swimming class
• Let B be college students enrolled in basketball class
• Let E be the entire variety of college students

Utilizing the identical approach as in drawback #1, we now have the next Venn diagram

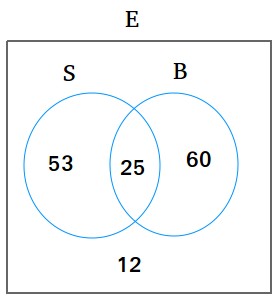
1. The variety of college students enrolled solely in swimming class is 53

2. The variety of college students enrolled solely in basketball class is 60

3. The variety of college students who’re neither enrolled in swimming class nor basketball class is 12

4. College students not enrolled in swimming class are enrolled in basketball class solely or are enrolled in neither of those two actions. In different phrases, every thing that’s not in S.

60 + 12 = 72

5. College students not enrolled in basketball class are enrolled in swimming class solely or are  enrolled in neither of those two actions. In different phrases, every thing that’s not in B.

53 + 12 = 65

6. The variety of college students enrolled in swimming class or basketball class is discovered by including something in S solely, in B solely and within the intersection of S and B?

53 + 25 + 60 = 138

A tough Venn diagram phrase drawback with two circles

Phrase drawback #3

In a survey of 100 folks, 28 folks smoke, 65 folks drink, and 30 folks do neither. How many individuals do each?

Resolution

• Let Okay be the quantity of people that smoke
• Let D be  the quantity of people that drink
• Let E be the entire variety of folks
• Let x be the quantity of people that smoke and drink

If we make a Venn diagram, here’s what we now have up to now.

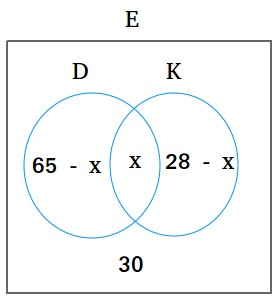
We find yourself with the next equation to unravel for x.

(65 – x) + x + (28 – x) + 30 = 100

65 – x + x + 28 – x + 30 – 30 = 100 – 30

65 – x + x + 28 – x  = 70

65 + 0 + 28 – x  = 70

93 – x  = 70

Since 93 – 23 = 70, x  = 23

The quantity of people that do each is 23.