30-60-90 Triangle
[ad_1]
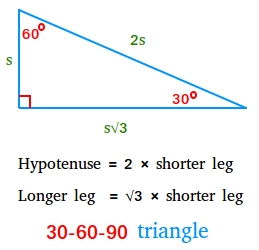
A 30°-60-90 triangle is a particular proper triangle by which the size of the hypotenuse is twice the size of the shorter leg. The size of the longer leg is the sq. root of three instances the size of the shorter leg.
Hypotenuse = 2 × shorter leg
Longer leg = √3 × shorter leg

Wanting rigorously on the determine above, you will have noticed the next ratios:
Suppose we begin from the smallest angle to the biggest angle and from the shortest aspect to the longest aspect
The angles of a 30-60-90 triangle are within the ratio 1:2:3
The edges of a 30-60-90 triangle are within the ratio 1:√3:2
30-60-90 triangle proof
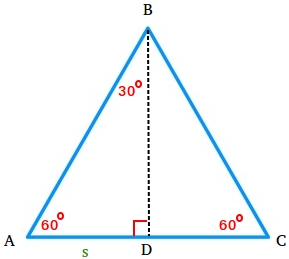
Begin with an equilateral triangle ABC the place every inside angle is the same as 60 levels.
Since section BD is the perpendicular bisector of section AC, we now have two 30-60-90 triangles.
Let section AD equal to s and use the Pythagorean theorem to search out the size of section BD.
Discover that AC = s + s = 2s. Since AB = AC, AB = 2s.
AD2 + BD2 = AB2
s2 + BD2 = (2s)2
s2 – s2 + BD2 = (2s)2 – s2
BD2 = (2s)2 – s2
BD2 = 4s2 – s2
BD2 = 3s2
BD = √(3s2)
BD = s√3
Examples of 30-60-90 triangles
Instance #1: 1, √3, 2
Quick leg: 1
lengthy leg: √3
Hypotenuse: 2
Instance #2: 2, 2√3, 4
Quick leg: 2
lengthy leg: 2√3
Hypotenuse: 4
Instance #3: 5, 5√3, 10
Quick leg: 5
lengthy leg: 5√3
Hypotenuse: 10
Utilizing the size of 1 aspect to unravel a 30-60-90 triangle
Instance #4:
The longer leg of a 30-60-90 triangle is 5. Discover the lengths of the opposite sides.
Longer leg = √3 × shorter leg
5 = √3 × shorter leg
Shorter leg = 5/√3
Multiply each numerator and denominator of 5/√3 by √3
Shorter leg = 5(√3) / √3(√3)
Shorter leg = 5(√3) / √9
Shorter leg = 5(√3) / 3
Hypotenuse = 2 × shorter leg
Hypotenuse = 2 × [5(√3) / 3]
Hypotenuse = 10√3 / 3
Utilizing the 30-60-90 triangle to unravel real-world issues
Instance #5:
The warning signal beneath is an equilateral triangle. Suppose the peak of the signal is 1 meter. Discover the size s of every aspect of the signal.

For the reason that triangle is an equilateral triangle, the altitude divides the triangle into two 30-60-90 triangles as proven within the determine beneath.
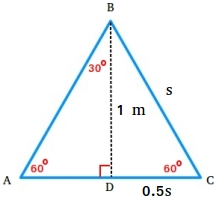
Discover that the size of the shorter leg is the same as (1/2)s or 0.5s for the reason that altitude additionally bisects the bottom.
1 = √3 × shorter leg
1 = √3 × 0.5s
Divide each side of the equation by 0.5
1/0.5 = (√3)s
2 = (√3)s
Divide each side of the equation by (√3)
2/(√3) = s
s = 1.15 m
The size of every aspect of the signal is about 1.2 m
Instance #6:
An escalator lifts folks to the second flooring, 40 ft above the primary flooring. The escalator rises at a 30 levels angle. How far does the particular person journey from the underside to the highest of the escalator?
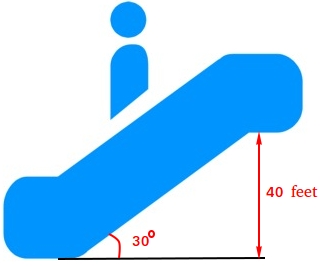
The determine above describes instance #6 with a 30-60-90 triangle. Discover that the shorter aspect is 40 ft and it’s reverse to the angle that measures 30 levels.
The space from the underside of the escalator to the highest is the size of the hypotenuse of the 30-60-90 triangle.
This distance is twice the size of the shorter aspect. Due to this fact, the space you journey is 80 ft.
Space of a 30-60-90 triangle
To search out the realm of a 30-60-90 triangle, simply be sure to get the peak of the triangle appropriately.
Remember the fact that both the longer aspect or the shorter aspect could possibly be the peak of the triangle. Simply use the method beneath:
Longer leg = √3 × shorter leg
If the shorter leg of the triangle is given, then the peak = √3 × shorter leg and the shorter leg is the bottom.
If the longer leg of the triangle is given, then the peak = longer leg / √3 and the bottom is the longer leg.
Instance #7:
Discover the realm of the 30-60-90 triangle beneath
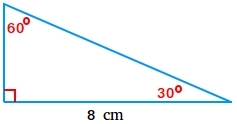
For the reason that longer leg is the bottom, peak = 8/√3 = 4.618
Space = 8 × 4.618
Space = 36.944
The world of the triangle is 36.944 cm2
[ad_2]